RSA Encryption: The Mathematical Foundation of Modern Cryptography
RSA Encryption
What is RSA Encryption?
RSA (Rivest-Shamir-Adleman) is a public-key cryptosystem that enables secure communication over insecure channels. Named after its inventors Ron Rivest, Adi Shamir, and Leonard Adleman, RSA relies on the mathematical difficulty of factoring large composite numbers into two prime numbers. It allows anyone to encrypt messages using a public key, but only the holder of the corresponding private key can decrypt them.
RSA (Rivest-Shamir-Adleman) is a public-key cryptosystem that enables secure communication over insecure channels. Named after its inventors Ron Rivest, Adi Shamir, and Leonard Adleman, RSA relies on the mathematical difficulty of factoring large composite numbers into two prime numbers. It allows anyone to encrypt messages using a public key, but only the holder of the corresponding private key can decrypt them.
The Problem RSA Solves: The Key Distribution Problem
The Classical Cryptography Dilemma
Before RSA, all encryption systems were symmetric - the same key was used for both encryption and decryption. This created a fundamental problem: How do you securely share the secret key with someone over an insecure channel?
Imagine Alice wants to send a secret message to Bob. With symmetric encryption, she first needs to secretly give Bob the key. But if they could communicate secretly to share the key, why not just send the original message that way? This circular problem plagued cryptography for centuries.
Before RSA, all encryption systems were symmetric - the same key was used for both encryption and decryption. This created a fundamental problem: How do you securely share the secret key with someone over an insecure channel?
Imagine Alice wants to send a secret message to Bob. With symmetric encryption, she first needs to secretly give Bob the key. But if they could communicate secretly to share the key, why not just send the original message that way? This circular problem plagued cryptography for centuries.
| Encryption Type | Key Structure | Key Distribution | Main Advantage | Main Disadvantage |
|---|---|---|---|---|
| Symmetric (Classical) | Single shared key | Must be shared secretly beforehand | Fast encryption/decryption | Key distribution problem |
| Asymmetric (RSA) | Public/Private key pair | Public key can be shared openly | Solves key distribution problem | Slower than symmetric encryption |
The Beautiful Idea: Public Key Cryptography
The Revolutionary Concept
RSA introduced the revolutionary idea of asymmetric cryptography:
The Magic: Messages encrypted with the public key can only be decrypted with the corresponding private key. This means anyone can send you encrypted messages, but only you can read them!
RSA introduced the revolutionary idea of asymmetric cryptography:
- Public Key: Can be shared with everyone - used for encryption
- Private Key: Kept secret by the owner - used for decryption
The Magic: Messages encrypted with the public key can only be decrypted with the corresponding private key. This means anyone can send you encrypted messages, but only you can read them!
Mathematical Foundation: Number Theory Concepts
Prime Numbers
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Examples: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47...
Fundamental Theorem of Arithmetic: Every integer greater than 1 can be represented uniquely as a product of prime numbers.
Example: $60 = 2^2 \times 3 \times 5$
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Examples: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47...
Fundamental Theorem of Arithmetic: Every integer greater than 1 can be represented uniquely as a product of prime numbers.
Example: $60 = 2^2 \times 3 \times 5$
Modular Arithmetic
We say $a \equiv b \pmod{n}$ (read as "a is congruent to b modulo n") if $n$ divides $(a - b)$.
Examples:
Think of it as clock arithmetic: On a 12-hour clock, 17 o'clock is the same as 5 o'clock.
We say $a \equiv b \pmod{n}$ (read as "a is congruent to b modulo n") if $n$ divides $(a - b)$.
Examples:
- $17 \equiv 5 \pmod{12}$ because $17 - 5 = 12$ is divisible by 12
- $25 \equiv 1 \pmod{8}$ because $25 - 1 = 24$ is divisible by 8
Think of it as clock arithmetic: On a 12-hour clock, 17 o'clock is the same as 5 o'clock.
Euler's Totient Function φ(n)
φ(n) counts the number of integers from 1 to n that are relatively prime to n (i.e., gcd(k,n) = 1).
For prime p: φ(p) = p - 1
For product of two primes: φ(pq) = φ(p)φ(q) = (p-1)(q-1)
Example: φ(15) = φ(3×5) = φ(3)×φ(5) = 2×4 = 8
The numbers relatively prime to 15: {1, 2, 4, 7, 8, 11, 13, 14}
φ(n) counts the number of integers from 1 to n that are relatively prime to n (i.e., gcd(k,n) = 1).
For prime p: φ(p) = p - 1
For product of two primes: φ(pq) = φ(p)φ(q) = (p-1)(q-1)
Example: φ(15) = φ(3×5) = φ(3)×φ(5) = 2×4 = 8
The numbers relatively prime to 15: {1, 2, 4, 7, 8, 11, 13, 14}
Euler's Theorem: The Heart of RSA
Euler's Theorem
If gcd(a,n) = 1, then: $$a^{\phi(n)} \equiv 1 \pmod{n}$$
Special Case - Fermat's Little Theorem: If p is prime and gcd(a,p) = 1, then: $$a^{p-1} \equiv 1 \pmod{p}$$
If gcd(a,n) = 1, then: $$a^{\phi(n)} \equiv 1 \pmod{n}$$
Special Case - Fermat's Little Theorem: If p is prime and gcd(a,p) = 1, then: $$a^{p-1} \equiv 1 \pmod{p}$$
Why Euler's Theorem Matters for RSA
This theorem gives us a way to "undo" exponentiation in modular arithmetic. If we can find exponents e and d such that $ed \equiv 1 \pmod{\phi(n)}$, then:
RSA Algorithm: Step-by-Step Construction
RSA Key Generation
Step 1: Choose two large prime numbers p and q
Step 2: Compute n = pq (this will be part of both keys)
Step 3: Compute φ(n) = (p-1)(q-1)
Step 4: Choose e such that 1 < e < φ(n) and gcd(e, φ(n)) = 1
Step 5: Find d such that ed ≡ 1 (mod φ(n))
Public Key: (n, e)
Private Key: (n, d)
Step 1: Choose two large prime numbers p and q
Step 2: Compute n = pq (this will be part of both keys)
Step 3: Compute φ(n) = (p-1)(q-1)
Step 4: Choose e such that 1 < e < φ(n) and gcd(e, φ(n)) = 1
Step 5: Find d such that ed ≡ 1 (mod φ(n))
Public Key: (n, e)
Private Key: (n, d)
RSA Encryption and Decryption
To encrypt message m: $c \equiv m^e \pmod{n}$
To decrypt ciphertext c: $m \equiv c^d \pmod{n}$
Why this works: $c^d \equiv (m^e)^d \equiv m^{ed} \equiv m \pmod{n}$ (by Euler's Theorem)
To encrypt message m: $c \equiv m^e \pmod{n}$
To decrypt ciphertext c: $m \equiv c^d \pmod{n}$
Why this works: $c^d \equiv (m^e)^d \equiv m^{ed} \equiv m \pmod{n}$ (by Euler's Theorem)
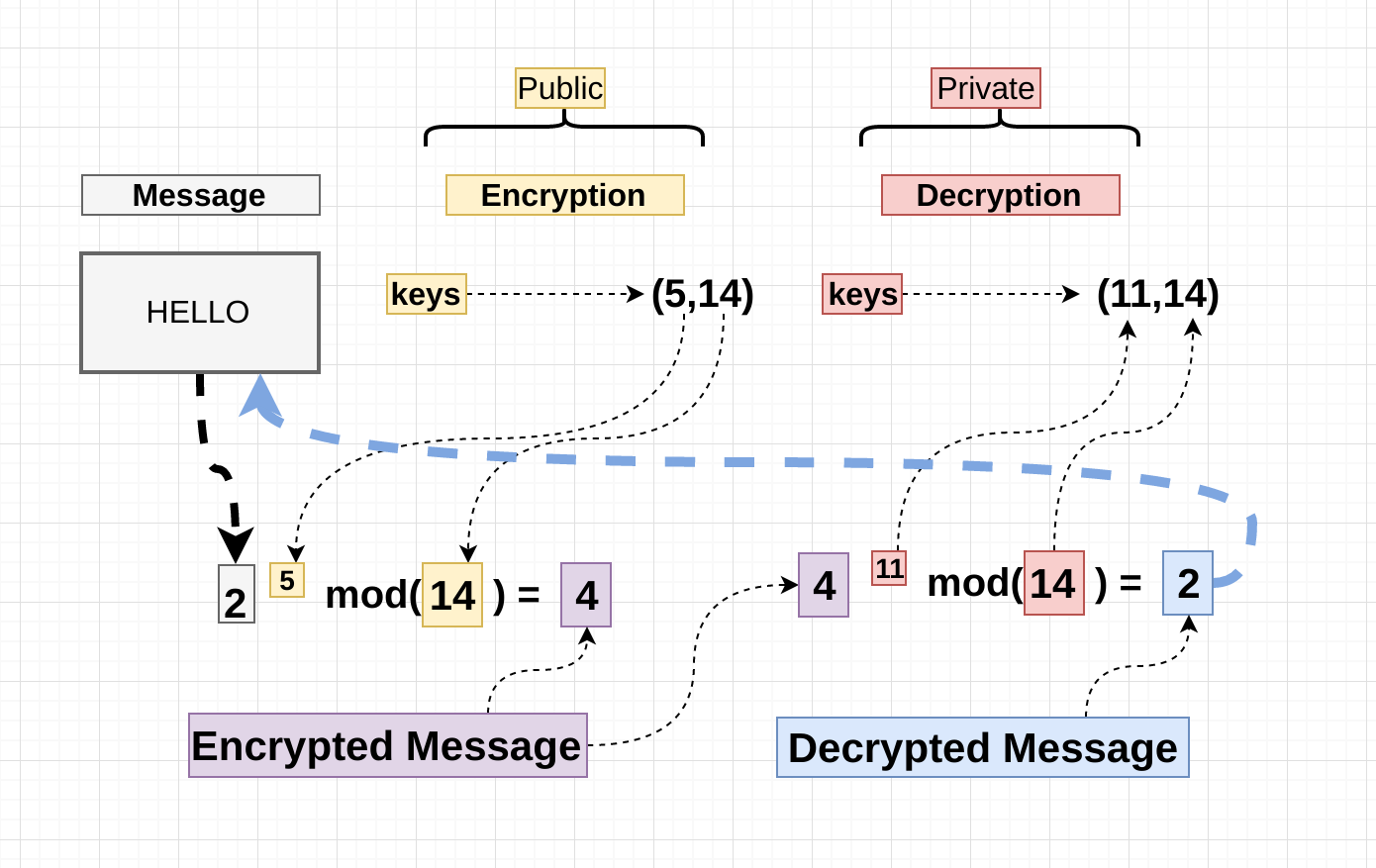
Worked Example: Small-Scale RSA
Let's build an RSA system step by step:
Finding the Private Key: Extended Euclidean Algorithm
The Extended Euclidean Algorithm
To find d such that ed ≡ 1 (mod φ(n)), we need to solve: $$ed + k\phi(n) = 1$$ for integers d and k.
This is equivalent to finding the multiplicative inverse of e modulo φ(n).
To find d such that ed ≡ 1 (mod φ(n)), we need to solve: $$ed + k\phi(n) = 1$$ for integers d and k.
This is equivalent to finding the multiplicative inverse of e modulo φ(n).
Extended Euclidean Algorithm Example
Security of RSA: Why It's Hard to Break
The Integer Factorization Problem
RSA's security relies on the fact that while it's easy to multiply two large primes together, it's extremely difficult to factor the result back into its prime factors.
Easy Direction: 1009 × 1013 = 1,022,117 (milliseconds on any computer)
Hard Direction: Factor 1,022,117 = ? × ? (could take years for large numbers)
RSA's security relies on the fact that while it's easy to multiply two large primes together, it's extremely difficult to factor the result back into its prime factors.
Easy Direction: 1009 × 1013 = 1,022,117 (milliseconds on any computer)
Hard Direction: Factor 1,022,117 = ? × ? (could take years for large numbers)
| Key Size (bits) | Decimal Digits | Security Level | Time to Factor (estimated) |
|---|---|---|---|
| 512 | 154 | Broken | Months (with modern hardware) |
| 1024 | 308 | Deprecated | Years to decades |
| 2048 | 617 | Current standard | Thousands of years |
| 4096 | 1234 | High security | Millions of years |
Real-World Applications
Where RSA is Used Today:
- HTTPS/TLS: Securing web traffic and online transactions
- Digital Signatures: Verifying the authenticity of documents and software
- Email Encryption: PGP/GPG systems for secure email
- VPNs: Establishing secure tunnels over public networks
- Code Signing: Ensuring software hasn't been tampered with
- Cryptocurrency: Bitcoin and other blockchain systems
Conclusion: The Elegance of Mathematical Security
RSA encryption represents one of the most elegant applications of pure mathematics to real-world problems. By leveraging the fundamental properties of prime numbers and modular arithmetic, it provides a foundation for secure communication that has enabled the digital age.
The beauty of RSA lies not just in its mathematical sophistication, but in its conceptual simplicity: anyone can encrypt, but only the intended recipient can decrypt. This revolutionary idea continues to protect billions of communications every day.
References
- Rivest, R., Shamir, A., & Adleman, L. (1978). A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2), 120-126.









