Elliptic Curve Cryptography: The Mathematical Beauty Behind Modern Security
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) is a form of public-key cryptography that uses the algebraic structure of elliptic curves over finite fields. Proposed independently by Neal Koblitz and Victor Miller in 1985, ECC provides the same level of security as traditional methods like RSA but with significantly smaller key sizes. This makes it particularly valuable for mobile devices, embedded systems, and any application where computational efficiency and bandwidth are crucial.
Why Elliptic Curves? The Efficiency Revolution
The primary advantage of ECC over traditional public-key systems like RSA lies in its efficiency. While RSA requires very large key sizes (2048-4096 bits) to achieve strong security, ECC can provide equivalent security with much smaller keys. For example, a 256-bit ECC key provides roughly the same security as a 3072-bit RSA key. This dramatic reduction in key size leads to faster computations, reduced storage requirements, and lower bandwidth usage.
| Security Level (bits) | RSA Key Size | ECC Key Size | Efficiency Gain |
|---|---|---|---|
| 80 | 1024 bits | 160 bits | 6.4x smaller |
| 112 | 2048 bits | 224 bits | 9.1x smaller |
| 128 | 3072 bits | 256 bits | 12x smaller |
| 192 | 7680 bits | 384 bits | 20x smaller |
| 256 | 15360 bits | 512 bits | 30x smaller |
Mathematical Foundation: What Are Elliptic Curves?
An elliptic curve over the real numbers is defined by the equation: $$y^2 = x^3 + ax + b$$ where $4a^3 + 27b^2 \neq 0$ (to ensure the curve is non-singular, meaning it has no cusps or self-intersections).
For cryptographic purposes, we work with elliptic curves over finite fields, typically:
- Prime fields $\mathbb{F}_p$: $y^2 \equiv x^3 + ax + b \pmod{p}$ where $p$ is a large prime
- Binary fields $\mathbb{F}_{2^m}$: More complex but computationally efficient for certain applications
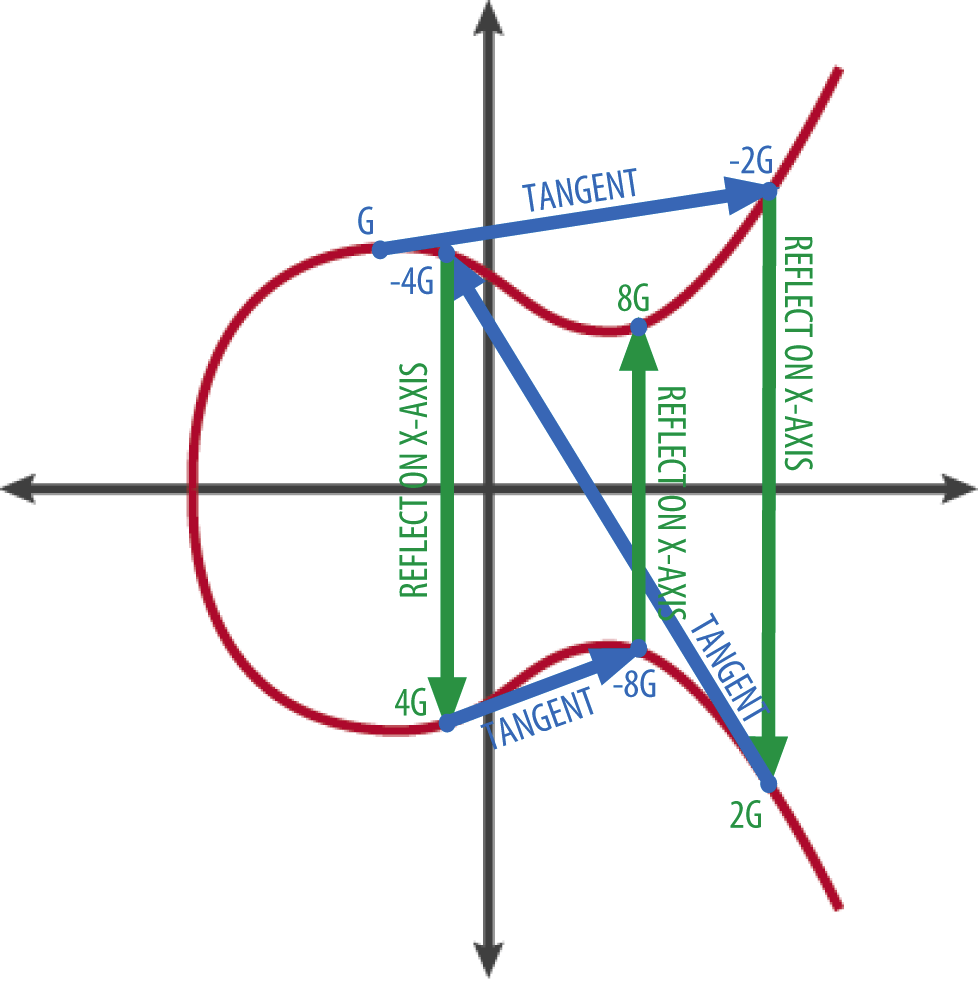
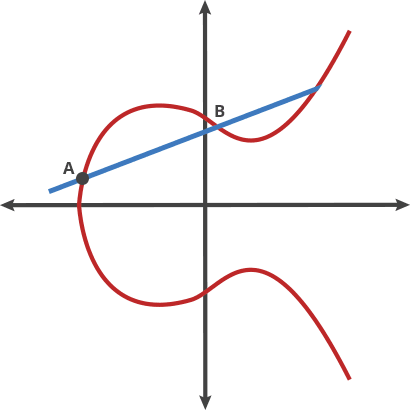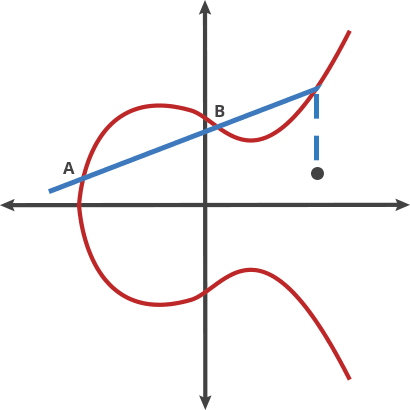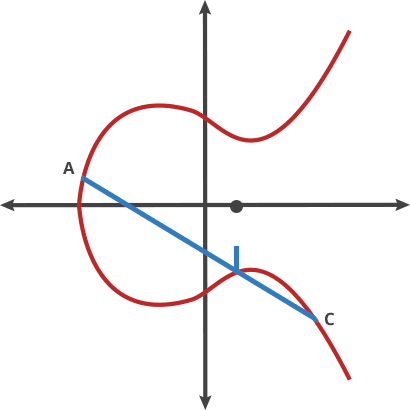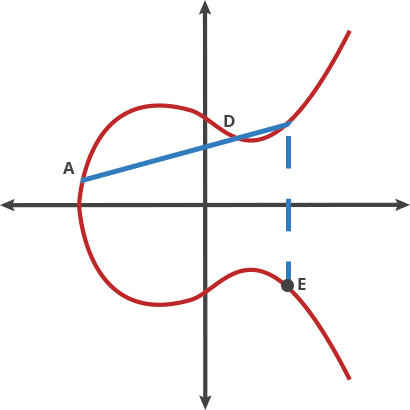
The magic of elliptic curves lies in their group structure. Points on the curve can be "added" together using a geometric construction:
Addition of two different points P and Q:
- Draw a line through points P and Q
- This line intersects the curve at a third point R'
- Reflect R' across the x-axis to get R = P + Q
Doubling a point P (P + P = 2P):
- Draw the tangent line to the curve at point P
- This tangent intersects the curve at another point R'
- Reflect R' across the x-axis to get R = 2P
The Point at Infinity: There's a special "point at infinity" denoted O that serves as the identity element: P + O = P for any point P.
For points $P = (x_1, y_1)$ and $Q = (x_2, y_2)$ on curve $y^2 = x^3 + ax + b$ over $\mathbb{F}_p$:
If P ≠ Q (Point Addition): $$\lambda = \frac{y_2 - y_1}{x_2 - x_1} \pmod{p}$$ $$x_3 = \lambda^2 - x_1 - x_2 \pmod{p}$$ $$y_3 = \lambda(x_1 - x_3) - y_1 \pmod{p}$$
If P = Q (Point Doubling): $$\lambda = \frac{3x_1^2 + a}{2y_1} \pmod{p}$$ $$x_3 = \lambda^2 - 2x_1 \pmod{p}$$ $$y_3 = \lambda(x_1 - x_3) - y_1 \pmod{p}$$
Then $P + Q = (x_3, y_3)$.
Why Do We Reflect Across the X-Axis? The Beautiful Logic of ECC Group Operations
We reflect across the x-axis because it's the mathematical "trick" that makes elliptic curves behave like a proper group. Without this reflection, the addition operation wouldn't be associative (meaning (P + Q) + R wouldn't equal P + (Q + R)), and we couldn't use elliptic curves for cryptography at all!
The Geometric Intuition
Let's think about this step by step. When we draw a line through two points on an elliptic curve, that line will intersect the curve at exactly one more point (this is guaranteed by the mathematical properties of cubic curves and that we know that a line would intersect the curve at most in three points). But here's the key insight: we want our addition operation to be "closed" - meaning when we add two points on the curve, we should get another point that's also on the curve and behaves predictably.
The Mathematical Reason: Group Theory Requirements
For elliptic curve points to form a group (which we need for cryptography), we must satisfy these properties:
- Closure: P + Q is always another point on the curve
- Associativity: (P + Q) + R = P + (Q + R)
- Identity: There exists a point O such that P + O = P
- Inverse: For every point P, there exists -P such that P + (-P) = O
The reflection is what makes properties 2 and 4 work correctly!
Why Not Just Use the Third Intersection Point Directly?
If we didn't reflect and just used the third intersection point directly, we'd run into problems:
Let's say we have points P and Q, and their line intersects at point R.
If we define P + Q = R (without reflection), then:
• What would be the "negative" of a point?
• How would we ensure (P + Q) + S = P + (Q + S)?
• The math quickly becomes inconsistent and unusable.
The Reflection Makes Everything Work
Step 1: Define the Negative
For any point P = (x, y) on the curve, its negative is -P = (x, -y).
This means every point has a clear inverse that's also on the curve!
Step 2: The Group Operation
When we draw a line through P and Q, it intersects at point R.
We define P + Q = -R (the reflection of R).
Step 3: Why This Works
Now the identity element is the "point at infinity" O.
For any point P: P + (-P) = O (they add up to "nothing")
And associativity holds: (P + Q) + R = P + (Q + R)
A Simple Analogy
Imagine the x-axis as the fulcrum of a see-saw. When you add two points on an elliptic curve:
- The line through them finds where they would "naturally" intersect
- But we want the result to "balance" the equation
- So we flip that intersection point across the fulcrum (x-axis)
- This flipping creates the mathematical balance that makes the group properties work
The Point Doubling Case
1. Draw the tangent line at point P
2. This tangent intersects the curve at exactly one other point, let's call it S
3. We define 2P = -S (the reflection of S across the x-axis)
Why the tangent?
When adding P + P, we can't draw a line through two distinct points (since they're the same point). The tangent line is the mathematical limit of the line through P and a point Q as Q approaches P.
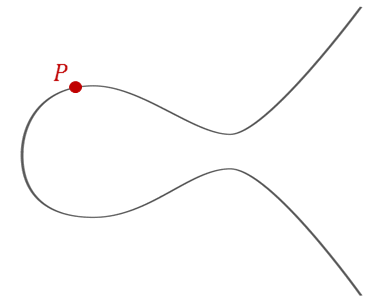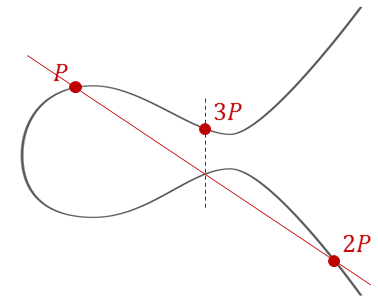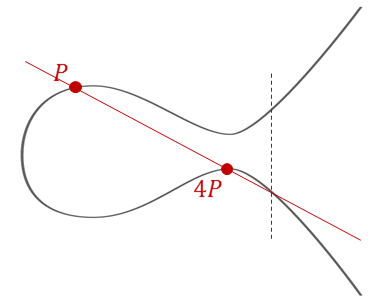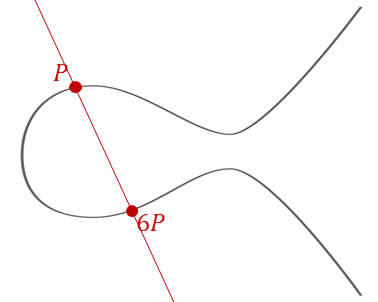
The Chain Continues: Finding 3P, 4P, etc.
1. We already know 2P (from the doubling process)
2. Draw a line through P and 2P
3. This line intersects the curve at point T
4. Then 3P = -T (reflection of T)
To find 4P:
1. We can either compute P + 3P, or 2P + 2P
2. Both methods give the same result (thanks to associativity!)
3. The reflection ensures consistency in both approaches
The Cryptographic Payoff
This reflection-based group operation is what makes the Elliptic Curve Discrete Logarithm Problem hard:
- Forward Direction (Easy): Computing kP = P + P + ... + P (k times) is efficient using "double-and-add" methods
- Reverse Direction (Hard): Given Q and P, finding k such that Q = kP requires solving the discrete logarithm problem
- The Group Structure: The reflection-based addition creates a complex, unpredictable sequence of points that makes the reverse direction computationally infeasible
Mathematical Elegance in Action
The reflection across the x-axis isn't just an arbitrary choice - it's a carefully designed mathematical operation that:
- Creates proper group structure: Makes elliptic curve points behave like a mathematical group
- Ensures consistency: Guarantees that addition is associative and has well-defined inverses
- Provides security: Creates the mathematical complexity that makes ECC cryptographically secure
- Maintains elegance: Keeps the geometric interpretation beautiful and intuitive
This is why mathematicians and cryptographers find elliptic curves so fascinating - they represent a perfect marriage of geometric beauty, algebraic structure, and practical security. The simple act of reflection transforms a geometric curiosity into the foundation of modern digital security!
The Elliptic Curve Discrete Logarithm Problem (ECDLP)
The security of ECC is based on the Elliptic Curve Discrete Logarithm Problem (ECDLP):
Given an elliptic curve E over a finite field, a base point G on the curve, and a point Q = kG (where k is a scalar and kG means G added to itself k times), it is computationally infeasible to find the integer k.
While computing Q = kG is efficient using techniques like "double-and-add," finding k given Q and G is extremely difficult. This asymmetry forms the basis of ECC security.
Simple Example: ECC over a Small Prime Field
Real-World Example: ECDH Key Exchange with secp256k1
ECC Algorithms in Practice
- Elliptic Curve Diffie-Hellman (ECDH): Key exchange protocol for establishing shared secrets. Used in TLS/SSL, VPNs, and secure messaging applications.
- Elliptic Curve Digital Signature Algorithm (ECDSA): Digital signatures for authentication and non-repudiation. Widely used in Bitcoin, Ethereum, and many PKI systems.
- Elliptic Curve Integrated Encryption Scheme (ECIES): Complete encryption scheme combining ECDH for key agreement with symmetric encryption for data.
- EdDSA (Edwards-curve Digital Signature Algorithm): Modern signature algorithm using Edwards curves, including Ed25519 used in SSH, Signal, and many cryptocurrencies.
Popular Elliptic Curves in Practice
| Curve Name | Field Size | Equation | Primary Applications |
|---|---|---|---|
| secp256k1 | 256-bit | y² = x³ + 7 | Bitcoin, Ethereum, cryptocurrencies |
| P-256 (secp256r1) | 256-bit | y² = x³ - 3x + b | TLS/SSL, NIST standard |
| Curve25519 | 255-bit | Montgomery curve | Signal, WhatsApp, SSH |
| Ed25519 | 255-bit | Edwards curve | SSH, Signal, digital signatures |
| P-384 (secp384r1) | 384-bit | y² = x³ - 3x + b | High-security applications, government |
ECDSA Digital Signatures: A Practical Example
Advantages and Limitations of ECC
- Smaller Key Sizes: Equivalent security with much smaller keys compared to RSA
- Faster Operations: More efficient computation, especially on mobile devices
- Lower Bandwidth: Smaller signatures and keys reduce communication overhead
- Battery Efficient: Less computational power required, important for IoT devices
- Forward Secrecy: Ephemeral ECDH provides perfect forward secrecy
- Curve Selection: Choosing secure curves is critical; some curves may have backdoors or weaknesses
- Implementation Complexity: More complex to implement correctly than RSA
- Side-Channel Attacks: Vulnerable to timing attacks and other side-channel vulnerabilities if not implemented carefully
- Quantum Vulnerability: Like all current public-key systems, ECC will be broken by sufficiently large quantum computers
- Patent Issues: Some ECC algorithms and optimizations are subject to patents
ECC in the Modern World
- Cryptocurrency: Bitcoin uses ECDSA with secp256k1 for transaction signatures. Ethereum uses the same curve for account authentication.
- Secure Messaging: Signal, WhatsApp, and iMessage use Curve25519 for key agreement and Ed25519 for signatures.
- Web Security: Modern browsers prefer ECDHE (Ephemeral ECDH) over RSA for TLS key exchange due to perfect forward secrecy.
- Mobile Devices: iOS and Android use ECC extensively for secure boot, app signing, and secure communications.
- IoT Security: Resource-constrained IoT devices rely on ECC for efficient public-key operations.
- Smart Cards: Credit cards, SIM cards, and identity cards use ECC for authentication due to space and power constraints.
The Future of ECC: Post-Quantum Considerations
While ECC provides excellent security against classical computers, it shares the same vulnerability as RSA and Diffie-Hellman to quantum computers running Shor's algorithm. A sufficiently large quantum computer could solve the ECDLP efficiently, breaking all current ECC implementations. This has led to active research in post-quantum cryptography, including lattice-based, hash-based, and code-based alternatives. However, ECC remains secure against current technology and will likely continue to be used for many years while post-quantum standards mature.
Elliptic Curve Integrated Encryption Scheme (ECIES)
ECIES is a hybrid encryption system. It uses Elliptic Curve Diffie–Hellman (ECDH) to agree on a shared secret, then splits that secret into two symmetric keys: one for fast encryption (e.g., AES) and one for message authentication (MAC). This combination gives you both confidentiality and integrity.
Key Pairs in ECIES
- Recipient’s Long-Term Key Pair:
Private key:n
Public key:P = n × G - Sender’s Ephemeral Key Pair:
Private key:e
Public key:E = e × G
Generated fresh for each message, then discarded.
Encryption Process (Sender)
- Get Recipient's Public Key:
The sender obtains the recipient’s long-term public key
P. - Generate Ephemeral Keys:
Pick a random ephemeral private key
e, computeE = e × G. - Compute Shared Secret:
S = e × P = e × (n × G) = (e × n) × G. - Derive Symmetric Keys:
The shared secret
Sis an elliptic curve point with x and y coordinates. A Key Derivation Function (KDF), such as HKDF with SHA-256, is used to turn these coordinates into cryptographically strong keys:input = x(S) || y(S) key_material = HKDF(input) k_enc = first 16 bytes # encryption key (AES-128) k_mac = next 16 bytes # MAC key
Why use a KDF? The raw coordinates ofSare not random bitstrings. A KDF extracts and expands them into secure, independent keys for encryption and authentication. - Encrypt & Authenticate:
- Ciphertext: Encrypt the plaintext (the actual data/message) using AES (or similar) with
k_enc:ciphertext = AES_Encrypt(k_enc, plaintext)
- MAC: A short tag that proves the ciphertext hasn’t been tampered with. Typically computed using HMAC-SHA256 withk_mac:mac_tag = HMAC(k_mac, ciphertext)
The MAC ensures the message’s authenticity and integrity. - Transmit: Send three things to the recipient:
E— ephemeral public keyciphertext— encrypted datamac_tag— authentication tag
Decryption Process (Recipient)
- Compute Shared Secret:
Use private key
nand sender’s ephemeral public keyE:S' = n × E = n × (e × G) = (n × e) × G. - Derive Symmetric Keys:
Apply the same KDF to
S'to recover identicalk_encandk_mac. - Verify MAC:
Compute:
HMAC(k_mac, ciphertext)
If it matches the receivedmac_tag, the ciphertext is authentic. Otherwise, reject the message. - Decrypt:
If the MAC is valid, decrypt:
plaintext = AES_Decrypt(k_enc, ciphertext)
and recover the original message.
Sender: S = e × P = e × (n × G) = (e × n) × G
Recipient: S' = n × E = n × (e × G) = (n × e) × G
Since e × n = n × e, S = S'. This property of elliptic curve multiplication enables ECDH — and by extension, ECIES.
Quick Reference
| Term | Meaning | Produced By | Purpose |
|---|---|---|---|
k_enc | Symmetric encryption key | KDF output from S | Encrypt/decrypt the message |
k_mac | Symmetric MAC key | KDF output from S | Generate/verify MAC |
ciphertext | Encrypted message | AES (or similar) with k_enc | Confidentiality |
mac_tag | Message authentication code | HMAC of ciphertext with k_mac | Integrity & authenticity |
Conclusion: The Elegant Balance of Security and Efficiency
Elliptic Curve Cryptography represents one of the most elegant achievements in modern cryptography, providing a perfect balance between security and efficiency. By leveraging the mathematical beauty of elliptic curves and the hardness of the discrete logarithm problem, ECC enables secure communication with unprecedented efficiency. From the Bitcoin blockchain to the secure messaging apps we use daily, ECC quietly protects billions of digital interactions while using minimal computational resources.
As we advance into an era of increasingly connected devices and quantum computing threats, understanding ECC becomes ever more important. Its mathematical foundation provides not just practical security solutions, but also demonstrates how pure mathematics can have profound real-world impact. The curves that mathematicians studied centuries ago now secure our digital lives in ways they never could have imagined.
References
- Koblitz, N. (1987). Elliptic curve cryptosystems. Mathematics of computation, 48(177), 203-209.
- Miller, V. S. (1985). Use of elliptic curves in cryptography. In Conference on the theory and application of cryptographic techniques (pp. 417-426). Springer.
- Hankerson, D., Menezes, A. J., & Vanstone, S. (2003). Guide to elliptic curve cryptography. Springer Science & Business Media.
- Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36-63.
- Bernstein, D. J. (2006). Curve25519: new Diffie-Hellman speed records. In International workshop on public key cryptography (pp. 207-228). Springer.









